When in Rome, your functions should do as the Romans do. Automatically.
It should come as no surprise to those acquainted with Swift that the language includes support for functional idioms. Swiftz is a library that attempts to implement some of the common abstractions found in functional programming languages and makes them available to the Swift world. However, Swift is still primarily an object-oriented (OO) language so such abstractions take a slightly different form than the ones in functional languages.
The main abstraction in the functional world is the function. Hopefully it is safe to assume that everybody who might be reading this article knows what a function is. However, functions not attached to a class might seem limiting to those accustomed to the object-oriented abstractions. Specifically, those with a background in object-oriented programming (OOP) might expect to be able to use their functions within a given context implicitly. The context of the function (or method if you prefer that word) is given by the class where the function is defined.
First of all, we need to clarify what we mean with the word “context.” In the object-oriented world, context means a set of variables associated with an instance of an object. Methods defined within the same class can operate on these variables. However, the context of an instance (or class) method is also determined by the behaviour the class implements. This second variety of context is the one we talk about when we use the phrase computational context in functional programming. This might seem a little too abstract right now, but don’t despair as we will dive into some examples soon.
One of the common places where we apply a function within a different context from where the function was originally defined is when working with promises. For this example we will use the BrightFutures library for Swift. For the uninitiated, here’s an example lifted and simplified from the library’s README.md:
User.logIn(username,password)
.onSuccess(doSomethingWithPosts)
The previous code snippet does exactly what we just described. It
takes a value within a computational context and applies a function to
it. In this case, the context is going to be the result of the
successfully completed login action in the future. The
doSomethingWithPosts function will be invoked within that
context. Concretely, the .onSuccess method of the future applies the
function once the Future has resolved. This method effectively
allows us to apply regular functions in contexts that have yet to be
resolved.
However, there are an infinite number of computational contexts where we might want to apply our functions. We have just explored one. The next example that immediately comes to mind is Swift’s built-in Optional type. As a quick recap, let us quote Apple’s documentation on them:
Optionals say either “there is a value, and it equals x” or “there isn’t a value at all."
This is yet another computational context that we can consider in the same way we considered the Future computational context. Hereafter, we will refer to values of the Optional type to represent a computational context where failure can be represented.
Luckily for us, applying regular functions within the context of an Optional has been baked into the Swift language. This is what is called Optional chaining in the language documentation. Function application in the context of possible failure (i.e. Optional) is done transparently in Swift. Let’s look at this snippet from Apple’s documentation on Optional chaining:
let roomCount = john.residence?.numberOfRooms
The residence property of the john object is an Optional. It might
or might not exist. However we can look up a property on it just
fine. In this example we are applying the numberOfRooms method on a
value with an Optional type. Let’s take a look at Apple’s
documentation again:
The fact that it is queried through an optional chain means that the call to
numberOfRoomswill always return anInt?instead of anInt.
This contains an interesting tidbit of information. numberOfRooms
does not return an Optional, but when applied to a Residence? now it
will return Int?. The compiler merely wraps the type of
numberOfRooms in an Optional. This works in exactly the same way
with Future’s onSuccess function as the return value of onSuccess
is a Future.
Let’s stop for a second and notice the common pattern between
BrightFuture’s onSuccess and Optional chaining. onSuccess will
take a function and return a new Future with the function applied
after the Future has resolved. Optional chaining will take a
function and return a new Optional with the function applied within it
if it is not nil. Let’s look at a diagram to make the pattern more
evident:
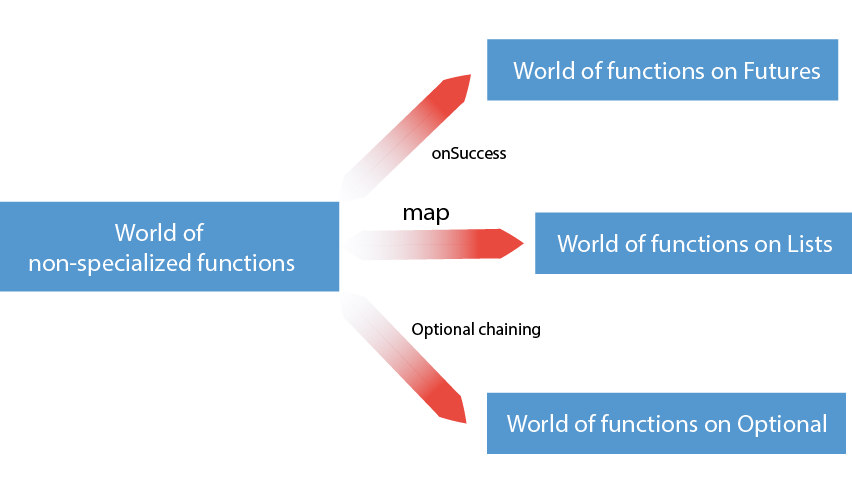
Let’s try to build some more intuition before we go deeper into the functional rabbit hole. Until now we have considered two different computational contexts: the context of possible failure modeled by Optional and the context of variables that do not have a value yet modeled by Future. It’s important to note that so far we have employed only regular functions to deal with both Optional and Future. In fact we could’ve used the same function for both examples. The most interesting part to notice here is that we never take care of the context by ourselves.
Enter Swiftz
Now we will look at another interesting computational context. This is
where Swiftz first comes into play. We will use Swiftz implementation
of list for this example. How do we apply a regular function to a
list? The answer is the map function. The relevant part can be found
in
Swiftz's source. In
order to apply a function to a list we simply map that function over
the list. The relevant code snippet:
public func map<B>(f : A -> B) -> List<B> {
switch self.match() {
case .Nil:
return []
case let .Cons(hd, tl):
return List<B>(f(hd), tl.map(f))
}
}
That is, we apply the function to every element in the list and return
a new list with the modified values. Now, it’s important to see if
this implementation fits within the framework of Optional and Future
we previously built. In the same way as Optional chaining and
onSuccess, map takes a value within a context (Optional, Future or
List so far) and a regular function and returns a new value within the
same context. We could say that optional chaining, onSuccess and
map are analogous operations. How are they related? They handle
the application of a plain old function within a computational
context.
Optional chaining, onSuccess and map are all examples of functors in
Swift. Intuitively, functors convert regular functions into
functions that can operate within a given computational context. This
is what we call "lifting". The functors shown so far have been
slightly different than those in the functional programming
world. Specifically, these Swift functors lift the function and then
immediately call the lift function with a value.
Functors in Swiftz are similar to the functors we have seen so
far. Swiftz defines a protocol for functors. A class that wants to
conform to the functor protocol mainly needs to implement the fmap
method. This allows us to call fmap on any object that conforms to
the protocol. At this point we should look at the code. First, the
Functor protocol from Swiftz:
public protocol Functor {
typealias A
typealias B
typealias FB = K1<B>
func fmap(f : A -> B) -> FB
}
In order to conform to this protocol a class needs to define two
typealiases and one method. fmap is the common name that corresponds
to both onSuccess in the case of futures and map in the case of
lists. The type aliases correspond to the types of the function we are
going to lift using the fmap definition. For now you can ignore the
third typealias. The type signature of the fmap function is the most
interesting part. fmap as defined in the protocol takes a function
and produces a value within the context of the functor. But wait,
isn’t something missing here? Shouldn’t fmap take a FA too? Isn’t
fmap supposed to take a function and a value? Well, in the way
Functors are implemented in Swiftz, fmap lifts the given function
and applies it to an instance value in the class where fmap is
defined. That’s where the missing FA went. Just to make it clearer
that fmap and map are equivalent in Swiftz when it comes to
lists, here's Swiftz's implementation of fmap for List:
extension List : Functor {
typealias B = Any
typealias FB = List<B>
public func fmap<B>(f : (A -> B)) -> List<B> {
return self.map(f)
}
}
As you can see, fmap simply calls map.
We need to go deeper: the Basis library
Functors in the Basis library are a little closer to what functors in the functional world look like. First of all, let’s take a look at Basis’ Functor protocol:
public protocol Functor {
typealias A
typealias B
typealias FB = K1<B>
class func fmap(A -> B) -> Self -> FB
}
The primary difference here is that fmap is no longer an instance
method; now it’s a class method. It follows that this fmap does not
depend on the object’s state, but it needs the value passed to it
explicitly. Here Self can be read as FA. It’s also important to
notice that this function is curried, which means we can partially
apply it. It follows that this particular definition of fmap can
lift a function and then assign it to an identifier for the lifted
function to be applied later.
Basis defines Maybe as its own alternative to Swift's built-in
Optional. The semantics are very similar to Optional. An Optional
might contain Just(Something) or it might contain Nothing. It is
no longer possible to use optional chaining to work with Maybe, so a
functor to the world of Maybe might prove useful. Here's how Basis
defines a functor for its Maybe type:
extension Maybe : Functor {
typealias B = Any
typealias FB = Maybe<B>
public static func fmap<B>(f : A -> B) -> Maybe<A> -> Maybe<B> {
return { m in
switch m.match() {
case .Nothing:
return Maybe<B>.nothing()
case .Just(let x):
return Maybe<B>.just(f(x))
}
}
}
}
Let’s use this functor to apply a function to the Maybe type in Basis:
// Notice how Maybe is not even mentioned in this function definition
func sumTwo(number: Int) -> Int {
return number + 2;
}
let liftedSumTwo = Maybe.fmap(sumTwo) // lift the function and name it liftedSumTwo. Swift infers the type as "Maybe<Int> -> Maybe<Int>"
let maybeNumber = Maybe.just(10) // define maybeNumber as a value with Maybe type
liftedSumTwo(Maybe.just(10)) // use the lifted function on the Maybe. Result: Maybe.just(12)
Notice how the function is first lifted and then applied. No need for immediate application as in the Swiftz’s case. We can even lift it, give it a name and then use it.
So which definition is right?
There's no right or wrong definition. The Swiftz definition might be appealing to those who like OOP. The Basis definition might be more appealing to those who already program in a functional language. Personally, I like Basis' definition as it is closer to Haskell's functors, but that's just like my opinion.
note: some parts of the functor definition and the kind definition have been omitted in the interest of simplicity. The main point of this blogpost is building up intuition when it comes to functors. It is not meant to be a rigorous exposition.



