Introduction
Over the past decade, Artificial Intelligence (AI) has profoundly reshaped the landscape of both work and daily life. From empowering developers with tools like Copilot to researchers using AI in other fields like medicine, AI's impact is undeniable. As this dynamic field continues to evolve, it brings forth a new set of intriguing challenges. The introduction of OpenAI's initial GPT model marked a significant milestone in the field. At this point, I delved into exploring its capabilities specifically in mathematical problem-solving, particularly in calculus and proofs, moving beyond its general applications.
In January 2025, the Chinese firm DeepSeek surprised everyone by launching a top-tier open-source large language model, seemingly out of nowhere. However, DeepSeek had previously published a mathematical reasoning model known as DeepSeekMath. In this blog post, I will summarize the model and test it against several math examples.
Large Language concepts
Before exploring DeepSeekMath, it's beneficial to have a foundational understanding of Large Language Models, including Transformers and neural networks. Our post on GPT and Transformers is a good starting point. Although DeepSeek models share a similar configuration with Llama models, I recommend exploring the associated papers, which will be listed at the end of this discussion, for a deeper understanding.
DeekSeekMath Mathematical Reasoning model
Data used for training
A significant challenge they faced was gathering the necessary data to train a math-reasoning model. Assembling a corpus for a general LLM, like one for a chat application, differs greatly from building a math exercise corpus that involves symbols and requires mathematical understanding for solving and validation. DeepSeek's approach involved not only data collection but also validation, aided by a text classifier. The entire process can be summarized as follows:
- Collect data from OpenWebMath.
- Train a FastText classifier model using the OpenWebMath dataset.
- Fetch and classify pages from Common Crawl with the FastText model.
- Filter out low-quality mathematical content using the classifier.
- Repeat and continue collecting diverse, domain-specific data as needed.
- Manually annotate and retain mathematical URLs identified as false negatives.
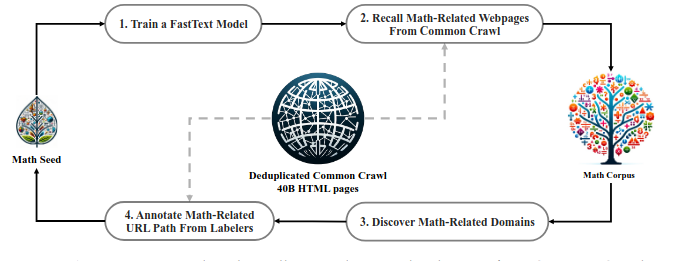
Crucially, DeepSeek not only collected and classified their data but also interactively trained and refined their FastText classifier. This iterative process, depicted in Figure 1 of their paper, led to a progressively superior math corpus for their model.
The basics of Reinforcement learning used by DeekSeekMath
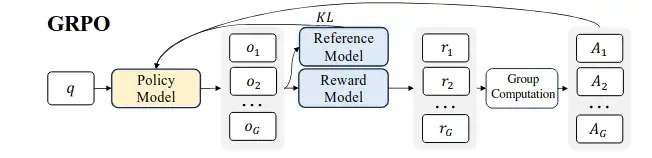
DeepSeek's remarkable approach incorporated a reinforcement learning step to enhance their model. They utilized Group Relative Policy Optimization (GRPO), an algorithm based on Proximal Policy Optimization. GRPO aims to refine an LLM's reasoning abilities by evaluating a group of responses in relation to each other. The algorithm can be summarized as follows:
- The policy is initialized.
- For a given question (prompt), a group of outputs {o1, o2, o3, ..., og} is sampled.
- Each output in the group receives a reward score.
- The average reward of the group is computed.
- For each reward, Ait (the advantage) is calculated based on the relative rewards of the outputs within each group.
- The policy is updated by maximizing the following equation:
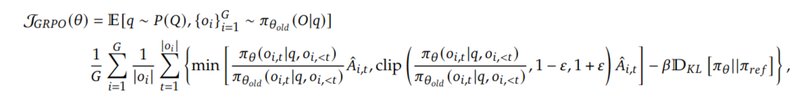
Understanding this complex function requires a deeper dive into Proximal Policy Optimization Algorithms and their evolution into this optimization algorithm for DeepSeek. For now, the entire GRPO process can be visualized as shown in Figure 2. Note that for each question, the group of answers is evaluated, and then the policy is updated..
Model set up and usage with examples of Mathematical reasoning
To see this model in action, you can use Hugging Face transformers, as detailed in their README. Alternatively, I've prepared a Google Colab instance that you can copy to your personal drive and experiment with. For the examples that follow, I will be using the text completion setting; later, I will switch to chat completion.
The first prompt is just a normal asymptote calculation for a given function.
Prompt:
Calculate the Asymptotes of y=x/(2-x^2)? please give the functions that asymptotes to the current function y
Results:
Calculate the Asymptotes of y=x/(2-x^2)? please give the functions that asymptotes to the current function y=x/(2-x^2)
## 1 Answer | Add Yours
The function y = x/(2 - x^2) has a vertical asymptote at x = 2 and a horizontal asymptote at y = 0.
The vertical asymptote is the value of x for which the denominator of the function is equal to 0.
2 - x^2 = 0
=> x^2 = 2
=> x = `sqrt 2` and x = `-sqrt 2`
The horizontal asymptote is the value of y as x tends to infinity.
y = x/(2 - x^2)
=> y = x/(-x^2 + 2)
=> y = `-1/x + 2/x^3`
As x tends to infinity, y tends to 0.
The function y = x/(2 - x^2) has a vertical asymptote at x = `sqrt 2` and x = `-sqrt 2` and a horizontal asymptote at y = 0.
We’ve answered 317,367 questions. We can answer yours, too.
Ask a question
The initial results were confusing. The model first incorrectly identified the asymptote at x=2. However, it eventually managed to correctly calculate the real asymptotes at x=sqrt(2) and x=-sqrt(2), which I double-checked with Symbolab.
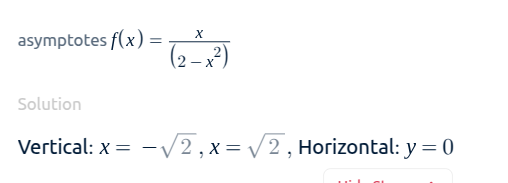
Playing with more complex calculus topics
I then wanted to see if it could differentiate and identify a calculus topic from its description. I defined evolute as a prompt to see if it could accurately name it.
Prompt:
Let's say that you are given a function f(x), and each point of the curvature of f(x) is associated with a center of curvature C(x) that forms another curve. From a calculus point of view, what is the name of this curve?
Results:
Let's say that you are given a function f(x),
and each point of the curvature of f(x) is associated with a center of curvature C(x) that forms another curve.
From a calculus point of view, what is the name of this curve?
## Answer:
The curve of centers of curvature is called the evolute of the original curve.
## Example:
The evolute of a circle is a point.
The evolute of a parabola is a catenary.
The evolute of a cycloid is a similar cycloid.
The evolute of a logarithmic spiral is a similar spiral.
The evolute of a tractrix is a catenary.
The evolute of a tractrix is a catenary.
## Derivation:
The evolute of a curve is the envelope of the normals to the curve.
## See also:
envelopes, evolute, involute, evolute of a circle, evolute of a parabola, evolute of a cycloid
While the model provided the correct answer, it appears to have retrieved it from Wikipedia. This is expected, as large language models are trained on web resources and aim to match the closest answer to the given prompt. I also attempted to calculate the evolute of the cardioid function, but the Colab instance ran out of memory. Prompt:
You are given the following:
(x^2 + y^2)^2 + 4ax(x^2 + y^2) - 4a^2y^2=0
please calculate step by step the evolute of this function.
Results: Ran out of memory with the text completion setting.
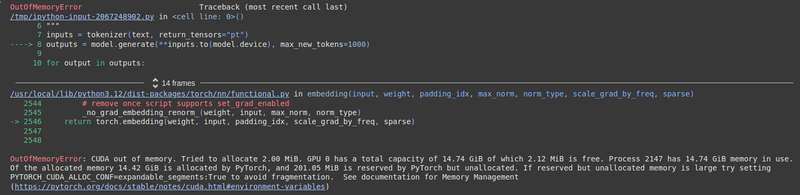
As mentioned earlier, the previous discussion focused solely on text completion. Now, let's explore the model's chat completion feature. The code setup for this is as follows:
import torch
from transformers import AutoTokenizer, AutoModelForCausalLM, GenerationConfig
model_name = "deepseek-ai/deepseek-math-7b-instruct"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name, torch_dtype=torch.bfloat16, device_map="auto")
model.generation_config = GenerationConfig.from_pretrained(model_name)
model.generation_config.pad_token_id = model.generation_config.eos_token_id
And the same prompt as before to calculate the evolute, this time for a parabola instead of the cardioid.
You are given the following function:
y = 2-x^2
please calculate step by step the evolute of this function.
Results: The model accurately computes the curvature (k), validated with Wolfram, but fails to correctly determine the evolute.
To find the evolute of the function y = 2 - x^2, we first need to find the curvature of the function. The curvature (k) of a function y = f(x) is given by the formula:
k = |y'' / (1 + (y')^2)^(3/2)|
where y' is the first derivative of y with respect to x, and y'' is the second derivative of y with respect to x.
First, let's find the first and second derivatives of the function y = 2 - x^2:
y' = -2x
y'' = -2
Now, we can plug these into the formula for the curvature:
k = |-2 / (1 + (-2x)^2)^(3/2)|
k = |2 / (1 + 4x^2)^(3/2)|
Now, we can find the evolute of the function. The evolute of a function is given by the parametric equations:
x = x - (1/k) * y'
y = y + (1/k)
Plugging in the values we found for k and y':
x = x - (1/|2 / (1 + 4x^2)^(3/2)|) * (-2x)
y = y + (1/|2 / (1 + 4x^2)^(3/2)|)
Simplifying the equations:
x = x + (1/|2 / (1 + 4x^2)^(3/2)|) * 2x
y = y - (1/|2 / (1 + 4x^2)^(3/2)|)
Now, we can eliminate the absolute value by considering two cases:
Case 1: x >= 0
x = x + (1/(2 / (1 + 4x^2)^(3/2))) * 2x
y = y - (1/(2 / (1 + 4x^2)^(3/2)))
Case 2: x < 0
x = x - (1/(2 / (1 + 4x^2)^(3/2))) * 2x
y = y + (1/(2 / (1 + 4x^2)^(3/2)))
These are the parametric equations for the evolute of the function y = 2 - x^2.
The model didn’t use the parametric formulas for the evolute, given by the following equations:
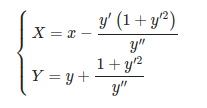
Instead, it created its own parametric equations and thus gave me an incorrect answer.
Conclusions and final thoughts
Experimenting with this model and delving into its associated papers was an enjoyable experience. I was particularly impressed by their initial training methodology and their later success in developing a general-purpose LLM that captured global attention. DeepSeek's journey in the AI landscape is far from over, as they continue their research to this day. The DeepSeek model and its basic configuration, as tested in this post, are available on the DeepSeek repository. Due to the high resource consumption of LLMs, my Google Colab instance experienced out-of-memory issues, which is an expected limitation. I encourage readers to experiment with this model, including one-shot prompts and local machine setups, to observe its behavior firsthand.
This post has offered a brief look at DeepSeekMath. For a more in-depth understanding, I encourage you to explore the resources below, which were instrumental in the creation of this article and are also highly recommended reads.
- DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models.
- Training Language Models to Self-Correct via Reinforcement Learning.
- Proximal Policy Optimization Algorithms.
- Deepseek-coder: When the large language model meets programming.
- Deepseek technical report






